In perspective drawing, a vanishing point represents a group of parallel lines, in other words, a direction.
In perspective drawing, a vanishing point represents a group of parallel lines, in other words, a direction.For any point on the paper, if we want a line towards the same direction (in the 3d space), we simply draw a line through it and the vanishing point.
But sometimes the vanishing point is too far away, such that it is outside the paper/canvas.
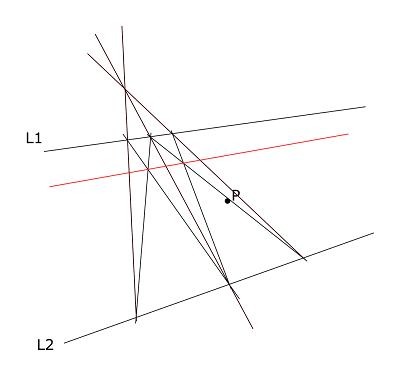
 In this example, we have a point P and two perspective lines L1 and L2.
In this example, we have a point P and two perspective lines L1 and L2.The vanishing point VP is naturally the intersection of L1 and L2. The task is to draw a line through P and VP, without having VP on the paper.
1. Use extra pieces of paper such that we can extend L1 and L2 until we see VP.
2. Draw everything in a smaller scale, such that we can see both P and VP on the paper. Draw the line and scale everything back.
3. Draw a perspective grid using the Brewer Method.
#1 and #2 might be quite practical. #3 may not guarantee a solution, unless we can measure distances/proportions.
Below I'll describe a method I learned in high school. It was more of a math quiz than a practical drawing method though, but it is quite fun.
To make it more complicated, there is an extra constraint for the drawer: you can only draw with a ruler without measurements, that is you can draw a straight line between two given points (assume that the ruler is long enough), but you cannot measure lengths or angles. You can not find middle points either (e.g. by folding the paper).
Here we go:

Step 1:
Draw two lines through P, cutting L1 and L2 at A1, A2, B1 and B2.
 Step 2:
Step 2:Draw two lines (A1, B2) and (A2, B1).
Find the intersection point Q.

Step 3:
Draw a line (Q, P), cutting L1 and L2 at A3 and B3 respectively.

Step 4:
Draw two lines (A1, B3) and (A3, B2).
Find the intersection P'.

Step 5:
Draw a line through P and P'.
This is the desired perspective line through P.
On the other hand, if we view Q as the second vanishing point, this figure represents a perspective view of a 2d rectangle (A1, A2, B1, B2). The rectangle is cut into two rectangles by the line (A3, B3). Note that (A1, B2), (A3, B3) and (A2, B1) are parallel lines in the 3d space.
Now it is clear that P is the center of the rectangle (A1, A2, B1, B2), P' is the center of the rectangle (A1, A3, B3, B2). Therefore the lines (A1, A2), (B1, B2) and (P, P') must be all parallel in the 3d space. In the perspective view they must all pass through a common vanishing point. This shows that the line PP' is the answer.
There are 2 special cases.
The first case is when Q is also far outside the paper. This may happen when P is near the center between L1 and L2.
Now the new line is closer to P, we can apply the method above on L2 (or L1) and the new line.
If the new line is still too far from P, a few iterations of bisection should be enough.
The other special case is when P is not between L1 and L2.
In this case we may use standard extension method, to find a new perspective line that is on the other side of P. A few iterations might be needed.
Finally we can apply the method above with the new line and L1.
There are still other cases where this method won't always work. For example, if L1 and L2 are close to the top and bottom edge of the paper, there is not much we can do. After all this was only a math quiz in the first place.
If the new line is still too far from P, a few iterations of bisection should be enough.
In this case we may use standard extension method, to find a new perspective line that is on the other side of P. A few iterations might be needed.
Finally we can apply the method above with the new line and L1.